Originally distributed at Reclamation, the 2022 Eastercon.
Dr Elma York has 5 Easter eggs and they are all of different weights:
1 & 2 together weigh 1.2 kg
2 & 3 together weigh 1.35 kg
3 & 4 together weigh 1.15 kg but
4 & 5 together weigh 0.8 kg and
1 & 3 & 5 together weigh 1.6 kg
What is the weight of any one of the eggs?Answer: Add together all of the egg weights, so 2 x egg 1+2 x egg 2+3 x egg3+2 x egg4+2 x egg5 weigh 6.1kg but 1 & 2 together weigh 1.2kg and 4 & 5 together weigh 0.8kg so, subtracting 2 each of eggs 1 & 2, and 4 & 5 means 3 x egg3 must weigh 2.1kg and egg3 weighs 0.7kg
Paul Atreides has been captured by Fremen who want to know if he is intelligent enough to waste water on. There is a main water tank, an empty 7 hrar and a 5 hrar container. Paul is allowed exactly 1 hrar of water per day which he needs to extract from the tank by filling the containers – with ‘spare’ water going back in the tank. If he takes more or less than the 1 hrar, or if he spills or drinks the water, they will kill him. What is the minimum number of times he must empty a container back into the main water tank in order to do this?
Answer: Once or twice. He fills the 5 hrar container from the tank, empties it into the 7 hrar and refills the 5 hrar and empties as much as he can (without spilling) into the 7 hrar container, filling it, leaving 3 hrar in the 5 hrar container. He empties the 7 hrar container back into the main water tank (first time) and puts the 3 hrar into the 7 hrar container. He then refills the 5 hrar container and empties as much as he can (without spilling) into the 7 hrar container, which leaves him with the 1 hrar he needs. He can then empty the 7 hrar container back into the main water tank (second time) and can drink his water. If he starts by filling the 7 hrar container, it takes a lot longer and requires more refilling of the main water tank.
Foul Ole Ron is quite mad, but has baffled all of the wizards. When he is freely offered a choice of two or more coins, he invariably takes the one of least value. Careful observation concludes that he does not decide based on the coin’s size, weight, thickness, diameter, colour, age or lustre but instead he consistently selects the coin that leaves him worse off than otherwise. Why?
Answer: Foul Ole Ron has realised that while he mystifies the courtiers by taking the least value coin, they will continue to give him coins from which to choose. Taking a higher value will mean they stop.
Fatma el-Sha’arawi asked me, ‘Can you find an average of two consecutive prime numbers that is also a prime?’
Answer: The average of any two numbers must lie between them. If they are consecutive primes, there cannot be a prime number between them.
Miles Vorkosigan is staying with a family on Barrayar which has three daughters. He is told that the product of their ages (them all multiplied together) is 36 and asked the ages of the daughters. He is unable to give the answer and asks for another clue. He is told that the sum of their ages is equal to the house door number. Still he is unable to answer and asks for yet another clue. He is told that the youngest daughter has bright blue eyes, and Miles nods and gives the correct answer. What is it?
Answer: The ages of the 3 daughters multiply to 36 which has many possible combinations of 3 factors e.g. 36 x 1 x 1 or 3 x 2 x 6, but he can’t tell, when they’re summed, which combination equals the door number, so it has to be a non-unique answer. Only 2 x 2 x 9 and 1 x 6 x 6 give an ambiguous answer. The fact that the youngest daughter has bright blue eyes, means that there is a youngest daughter, not twins.
I invited James Holden and Naomi Nagata to an Easter egg party. James brought 6 eggs and Naomi brought 3, but I’d forgotten the arrangement and brought none. We ate all of the eggs equally and I offered my friends £9 in compensation for the eggs. James said, ‘That’s £3 for me and £6 for Naomi.’ But I said, ‘That’s not fair!’ What would be fair?
Answer: I ate 3 of the eggs James brought. James and Naomi each ate 3 of their own eggs. Therefore, I owe all £9 to James.
Han Solo was in a cantina where the aliens were playing games of chess and dominoes. He observed to Chewbacca that the rectangular dominoes exactly covered two of the chessboard squares. Chewie promptly took two coins and put each one on the diagonally opposite corner squares of a chess board. He then asked Han in a series of grunts whether he could cover the rest of the chessboard with dominoes lain flat that did not overlap with the coins, each other or extend over the edge of the board. Can you?
Answer: The diagonally opposite corners of a chessboard are the same colour. A domino will cover 2 squares – one of each colour but there must be a discrepancy between the colours of 2 because of the coins: 30 white squares and 32 black or vice versa, so the dominoes cannot possibly cover all of the vacant squares.
Alison, Brian, Caroline, James and Zi are eating breakfast. Who is lucky enough to get mushrooms?
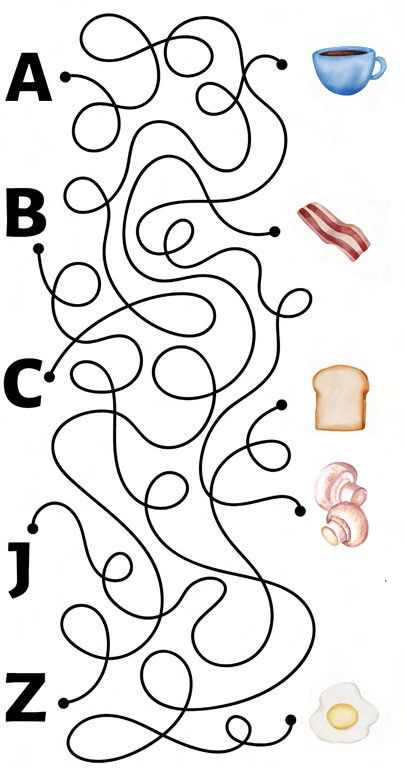
Answer: Alison (obviously) gets mushrooms for breakfast.
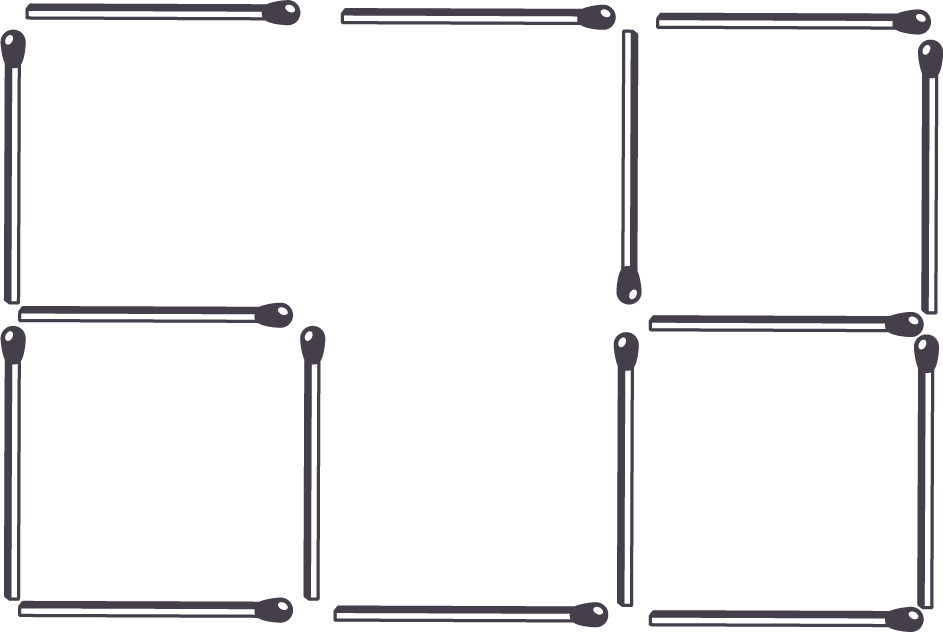
Can you move one match to make four complete squares with no matches left over?

Answer:
Colour in our lovely Conversation logo! You can see how Sue did it on our business cards, but we want to see what you can come up with.


